выиграть всего одну единицу условного капитала

Аналогичным образом можно сделать расчет и для других соотношений z и w . Но мы особо выделим случай более чем 10-кратного увеличения начального капитала при той же цели. Здравый смысл подсказывает, что вероятность выигрыша должна быть гораздо выше, чем была.

Пример Б : условия те же, что и в предыдущем примере, но z = 99.

Другими словами, представим, что трейдер обладает капиталом, который в 11 раз больше, чем в предыдущем примере. Но цели ставятся столь же скромные: выиграть всего одну единицу условного капитала, т.е. 30 базисных пунктов (тогда w = 100),

Получаем следующие оценки.

Математическое ожидание результата:

E ( w = 10) = -17,2.

Вероятность разорения:

Q ( z = 0) = 0,182. Вероятность достижения цели:

P ( w = 100) = 0,818. Средняя продолжительность игры:

D ( z = 0/ w = 100) = 172 испытания.

Как и ожидалось, столь серьезное увеличение начального капитала действительно повышает вероятность выигрыша, поскольку больший капитал малыми порциями труднее проиграть.

Однако неожиданным является то обстоятельство, что это увеличение не является существенным: оценка вероятности возрастает лишь незначительно с 0,79 до 0,82. Вместе с тем, усилий на выяснение отношений с рынком потребуется затратить непропорционально больше, чем в предыдущем примере: среднее число испытаний здесь 172, а там всего 11. Риторический вопрос: стоит ли овчинка выделки?

Таким образом, явное предпочтение следует отдать варианту действий по условиям примера А.

Относительный рост начального капитала в сравнении со ставкой повышает вероятность выигрыша, но в среднем потребует непропорционально больших усилий для достижения той же цели.

Принципиально важно подчеркнуть, что игра с применением этих расчетов на основе теории вероятностей обязана соблюдать важнейшее ограничение: необходимость обязательного выполнения заранее рассчитанного объявления стоп на продолжение прибыльных операций.

Если игрок, добившийся расчетного выигрыша, желает продолжить игру в том же формате, то он должен сделать соответствующую переоценку вероятности разорения и выигрыша. В противном случае ожидание столь же благоприятного результата при сохранении прежнего порядка игры ничем не оправдано, если, конечно, базироваться именно на рациональном подходе. Должны учитываться изменения исходного целеполагания и соответствующие коррекции остальных параметров задачи. Рассмотрим такой пример.

Пример В. Условия примера А, но с изменением цели выигрыша в сторону увеличения до w = 11. Иначе говоря, после первого успеха трейдер решил рискнуть еще раз и выиграть дополнительно одну единицу условного капитала. Получаем вероятность разорения:

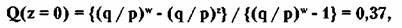
где q / р = 0,55 / 0,45; w = ll ; z = 9

Вероятность достижения цели w = 11:

P ( w = ll ) = l - Q ( z = 0) = 0,63. Математическое ожидание результата:

E ( w = 11) = 11 х 0,63 - 9 = -2,1.

Средняя продолжительность игры:

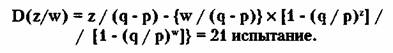
Нетрудно заметить, что все показатели ухудшились, хотя и остаются пока благоприятными (если вовремя остановиться).

Читатель может проверить самостоятельно, что третья попытка добиться успеха и довести начальный капитал до w =12 будет характеризоваться вероятностью достижения этой цели, уменьшенной уже до 0,5.

В этом смысле сделанные расчеты вступают в прямое противоречие с наставлениями, рекомендующими придерживаться именно того порядка работы, который хорошо зарекомендовал.

Как видим, подобные ожидания не имеют оснований. На самом деле не обходимо учитывать вероятностные оценки и на их основе ставить ордер стоп-операция по прибыли.