вероятность разорения для того, кому успех обеспечен по математическому ожиданию
Опуская математические выкладки, отметим,
что при неизменности начального капитала постепенное увеличение ставки
приводит к уменьшению вероятности разорения обреченного игрока. Соответственно,
вероятность разорения для того, кому успех обеспечен по математическому ожиданию,
увеличивается.
Это правило можно сформулировать так:
* в повторяющейся игре с постоянной ставкой
вероятность разорения игрока будет минимальной при выборе такой ставки, которая
была совместимой с суммой желаемого
выигрыша.
При неизменности начального
капитала и повторяющейся игре с постоянной ставкой вероятность разорения будет
минимальной при выборе такой ставки, которая была бы совместимой с суммой
желаемого выигрыша.
Пример 2. Рассмотрим ту же невыгодную
игровую ситуацию, при которой q = 0,55, р = 0,45. И пусть z = 90, a w = 100
условных единиц.
Если при каждом испытании ставка будет
равной одной условной единице, то вероятность разорения, действительно,
составит почти предельную величину:
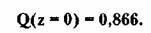
Но если увеличить ставку до максимально
возможного значения (при заданных условиях оно равно w - г = 100 - 90 = 10),
то столь неблагоприятный прогноз меняется кардинально. И хотя математическое
ожидание выигрыша остается тем же, вероятность разорения составит всего лишь
0,210, а выигрыша — возрастет до 0,790.
Как видим, несмотря на неблагоприятное
соотношения р и q , у обреченного игрока есть значительные шансы выйти
победителем в какой-то из попыток.
Разумеется, эту победу можно сохранить лишь
тогда, когда игрок имеет право тут же раскланяться и удалиться подальше от
места игры.
2. По существу, близкие к этим результаты
можно получить и для испытаний с идеальной монетой ( q = p ).
Правда, вышеприведенная формула оценки
вероятности разорения здесь не годится. Выведена более простая:
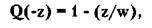
где ( w - z ) > 0 — чистый выигрыш. Тогда
вероятность такого исхода:
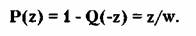
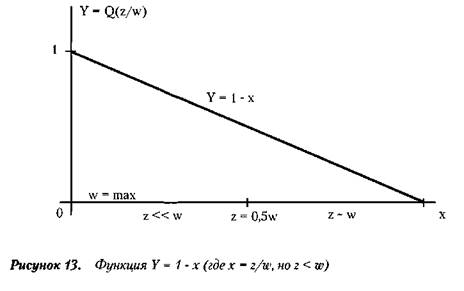
Если исследовать зависимость функции Q ( z /
w ) от соотношения переменных z и w , то обнаруживается следующее (см. рисунок
13).
При некотором заданном постоянном значении z
( z = const ) вероятность разорения уменьшается по мере изменения величины w в
сторону сближения с z . И вероятность разорения достигает минимальных
значений, когда величины w и z становятся сравнимыми ( z ~ w ).
Это правило можно сформулировать таким
образом:
• вероятность разорения в игре с постоянной
ставкой становится минимальной при малом в сравнении с исходным капиталом z
выигрыше как цели игры и максимально
приближенной к чистому выигрышу ( w - z ) ставке.
При р = q вероятность
разорения Q становится минимальной, а выигрыша Р — максимальной при двух
условиях: 1) минимальная цель выигрыша; 2) максимальная ставка.
Пример 3. (это условия примера 2, но только
для значения q = p ). При ставке, равной 0,lz, получим, что:
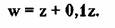
И тогда вероятность разорения
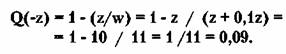
А вероятность выигрыша
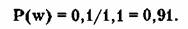
Статья размещена в рубрике: Модели торговых систем
| 
