вероятность разных сочетаний успеха и неудачи

Рассмотрим расчет по этой модели для частного случая, когда шансы на то, что сигнал окажется истинным или ложным, равны 50:50 (вероятность каждого исхода У 2 )*. Поинтересуемся, какова вероятность разных сочетаний успеха и неудачи, если испытание будет состоять из 3 попыток.

Начнем с того, что построим пространство элементарных событий.

Оно будет содержать:

2Г = 23 = 8 элементов.

Это такие сочетания:

•        успех, успех, успех;

•        успех, успех, неудача;

•        успех, неудача, успех;

•        неудача, успех, успех;

•        успех, неудача, неудача;

•        неудача, успех, неудача;

•        неудача, неудача, успех;

•        неудача, неудача, неудача.

Подчеркнем, что каждое из этих сочетаний является элементарным событием. Но напомним, что это верно только при испытании, которое определено как три попытки применения сигнала.

Следующий шаг: оцениваем вероятности этих элементарных событий.

Согласно принятой модели случайности исхода сработал — не сработал, нет причин, по которым одно сочетание, принадлежащее данному ПЭС, может быть вероятнее другого**. Поэтому вероятность каждого из них приравнивается к одному и тому же значению l / s (всего восемь событий, и все равно возможны).

Теперь, наконец, можно приступать к оценкам вероятности любых интересующих сложных (составных) событий в рамках имеющегося перечня в ПЭС.

Для примера рассмотрим вероятность такого события: имеет место хотя бы один успех.

Под это определение подходят варианты из ПЭС с любым числом успехов. Но не годятся те, где все три попытки — неудачные.

Тогда доля элементарных событий, попадающих под это определение, охватывает область из 7 элементов (все, кроме варианта неудача, неудача, неудача). В соответствии с этим вероятность интересующего события имеет место хотя бы один успех будет равна 7/8.

Можно посчитать, что такова же вероятность (7/8) и события: имеет место хотя бы одна неудача.

Оба события (хотя бы один успех и хотя бы одна неудача) являются зависимыми и совместимыми.

Оценим вероятности умножения и сложения этих двух событий.

Умножение означает новое событие, которое определено как хотя бы один успех и хотя бы одна неудача. На основе анализа ПЭС можно видеть, что этому условию в списке удовлетворяют б событий, т.е. все, за исключением первого (все успехи) и последнего (все неудачи). Тогда:

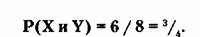
Сложение означает новое событие, которое определено так: либо хотя бы один успех или неудача, либо и то и другое. На основе анализа ПЭС можно видеть, что этому условию в списке удовлетворяют все события, входящие в ПЭС, т.е. вероятность Р( Х или Y либо X и Y ) = 1. Проверяем по соответствующей формуле:

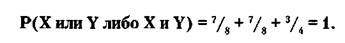
Это означает: что-нибудь да обязательно произойдет.

И еще пример, на котором мы здесь остановимся, поскольку он имеет значение для последующего рассмотрения.

Это оценка вероятности события: имеет место, по крайней мере, два успеха подряд. Данное событие охватывает три элементарных события:

•        успех, успех, успех;

•        успех, успех, неудача;

•        неудача, успех, успех.

Тогда соответствующая вероятность равна 3/ g .

Увеличим число успехов до максимума. Получим, что вероятность такого события (три успеха подряд) равна */8.

Если представить испытание как не три, а большее количество попыток, то легко видеть, что чем оно больше, тем еще более мизерной становится вероятность безошибочности. Так, при 20 операциях она меньше одной миллионной.

В этой связи уместно было бы вновь обратить внимание на принципиальное отличие дополнительного измерения, где, согласно принятым допущениям, действует чистый случай, от дурной неопределенности традиционных пространств. Так, в поведении рынка нередко можно обнаружить несколько десятков отдельных движений подряд в одну и ту же сторону*, что является крайне маловероятным событием. Поэтому и существуют оппоненты теории случайного рынка.

Однако не найдется даже ничтожно малой горстки трейдеров, которые в дополнительном измерении эффективности системы своей работы имели, хотя бы изредка, пусть не десятки, а полдюжины успехов подряд. Данный факт мы рассматриваем как косвенное подтверждение достаточной приближенности к реалиям представления о случайности событий в дополнительном измерении.

Сопоставление вероятностных расчетов с эмпирическими данными об эффективности существующих систем принятия торговых решений косвенно подтверждают случайный характер дополнительного измерения.