успешный порядок действий обладает магнитными свойствами

Продолжительное использование в пространствах случайных событий такого порядка работы с «равнонастроенным сигналом» (dSP = dSL), который, допустим, временно сумел себя хорошо зарекомендовать, вероятнее всего, приведет к последующему ухудшению результатов и в итоге - к разорению.

Вместе с тем, если трейдер удачлив не в меру, то благоприятная кривая арксинуса может быстро привести его к светлому будущему. И наоборот, даже при условии расчетной вероятности разорения равной всего 0,1 невезучесть игрока может преподнести ему самые неприятные сюрпризы.

К сожалению, всякий успешный порядок действий обладает магнитными свойствами. Психологически весьма трудно отказаться от того метода, который вот только что работал отменно. Такой подход вполне оправдан в детерминистическом мире, где существует пространственно-временная определенность ожидаемых результатов.

А в мире случайных событий — свои законы, согласно которым результаты, скорее всего, будут плавать. И если этого не учитывать, то можно попасть в ловушку неверных представлений, которые не подтверждаются ни вероятностными расчетами, ни реальным ходом событий.

В пространстве случайных событий факт возникновения периода эффективности в работе какого-то метода не гарантирует столь же благоприятных результатов и на все остальное будущее.

Наконец, кратко остановимся на оценках применения объявления стоп-операция для соотношений dSP и dSL , где они не равны между собой. Это уже другая настройка сигнала, которая из-за невыполнения условия dSP — dSL требует вывода иных способов оценки.

Поскольку при таком соотношении прямое приложение решений задачи о разорении невозможно, мы приведем эти условия к соответствующему эквиваленту, который будет применим. Для этого необходимо рассчитать новые значения dSP = dSL и соответствующие величины вероятностей р и q , которые давали бы те же оценки математического ожидания, что и для исходных условий dSP и dSL .

Последовательно сделаем это следующим образом.

1) Расчет q и р для заданного соотношения dSP < dSL :

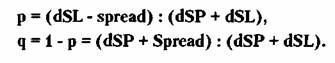
2) Оценка математического ожидания для dSP < dSL :

E = pxdSP - qxdSL .

3) Расчет эквивалентных значений dSP = dSL , которые давали бы то же
значение математического ожидания:

р xdSP - q xdSL = pxdSP - qxdSL .

Это уравнение можно представить как два:

р X dSP = р X dSP и q " xdSL = р х dSP .

Кроме того, естественно, должно выполняться условие:

p + q - i .

В результате решения этих уравнений, где в качестве неизвестных выступа ют р , q и dSP = dSL , получим формулы определения необходимых эквивалентных значений:

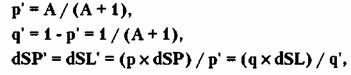
где под коэффициентом А обозначено выражение: А = (р / q ) x ( dSP / dSL ).

Здесь dSP = dSL представляют собой единицу условного капитала, ко торый выигрывается или проигрывается в каждом испытании, соответствен но, с вероятностью р и q . Именно эти значения мы и будем использовать, чтобы получить необходимые оценки по задаче о разорении при различных соотношениях dSP и dSL .