Успех в дополнительном измерении

Число успехов как случайная величина. Под случайной величиной понимается переменная, которая определена на пространстве элементарных событий через исходы некоторого опыта или эксперимента.

Роль такой случайной величины в нашем рассмотрении играет показатель к (число успехов).

Практический интерес для нас при исследовании процесса случайного поведения эффективности, показатель которой выражается в значении к, представляют вопросы, которые связаны, прежде всего, со следующими характеристиками:

1)            вероятность достижения суммарного успеха (величина к) вне зависимости от особенностей того или иного сочетания разных исходов, а также закономерные отклонения от ожидаемых величин;

2)     вероятные конфигурации кривой эффективности, которые могут складываться по ходу испытаний.

Очевидно, что число успехов (к) может случайным образом изменяться в каждой серии г одних и тех же испытаний Бернулли в пределах от 0 до г.

При этом особенно важно отметить, что одному и тому же значению переменной к могут соответствовать разные конфигурации (профили) графика эффективности.

Число успехов в биномиальных испытаниях — это случайная величина. При этом одному и тому же значению к могут соответствовать графики различной конфигурации (профилей).

Наиболее вероятное значение. Каждое значение к , будучи случайной величиной, может характеризоваться своей вероятностью возникновения. По этому можно полагать, что в каждой модели существуют некие наиболее вероятные значения к . Слишком большие отклонения величины к от этих наиболее вероятных значений в какой-то конкретной серии испытаний менее вероятны, чем маленькие.

Следует подчеркнуть различие между вероятностью некого числа ус пехов Р( к) и вероятностью успеха р в каждом отдельном испытании.

Напомним, что важнейшей особенностью чистого случая является независимость вероятности успеха (р) в каждом отдельном испытании от истории предыдущих результатов. Соответственно вероятность неуда чи q = 1 - р.

Нас интересуют вероятностные оценки P ( k / r / p ) в зависимости от трех переменных:

•        числа успехов к;

•        исходных значений q и р в биномиальных испытаниях;

•        длины серии г .

В рамках модели случайности можно рассматривать поведение кривой эффективности какого-то заданного сигнала, имеющего определенную оболочку и конкретную настройку (по прибыли и убытку).

Одна из частных, но практически важных моделей — это идеальная монета, где

p = q = 0,5.

Для модели разновеликая монета соотношение р : q может быть любым.

Как мы уже ранее видели, изменения априорных вероятностей* р и q зависит от настройки сигнала.  Априорная (а priori) вероятность — это оценка, теоретически принятая или исчисленная до появления эмпирических данных по результатам проведенных опытов. Вероятность, полученная эмпирическим путем, называется апостериорной (а posteriori).

О способе теоретического расчета этих значений речь пойдет несколько позже. Что же касается эмпирических значений р и q , то их можно получить по результатам наблюдений числа успехов к в заданной серии испытаний г:

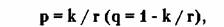
где к — число успехов в г проведенных испытаниях.

Учтем, что число неудач будет равно (г - к). Соответственно суммарный баланс (число успехов минус число неудач) можно представить в виде выражения:

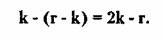
Допустим, что может быть проведено N серий по г испытаний в каждой. При этом результаты каждого испытания обозначим соответствующим век тором эффективности в дополнительном измерении, где:

•        на оси абсцисс откладывается порядковый номер испытания (от i до г);

•        на оси ординат — суммарный результат, т.е. текущая балансовая разница между абсолютными значениями успехов и неудач.

Тогда результаты каждой серии испытаний предстанут на графике в виде кривой случайного блуждания длиной в г векторов. Проведя аналогию между г и временем Т, а также между балансовым результатом (2к - г) и пространством перемещения, можно говорить о пространственно-временном графике блуждания.

Если (2к - г) > 0, то точка блуждания находится в положительной части пространства (правая верхняя четверть). При (2к - г) < 0 точка находится в отрицательной половине (правая нижняя четверть).

Для каждой нулевой отметки (нахождение точки блуждания на оси абсцисс) справедливо равенство 2к = г.

Это означает, что число успехов и неудач будет равным при условии четности количества испытаний.