Условная вероятность

 Представим ПЭС как объединение двух непересекающихся (независимых) множеств событий X и Y .

Пусть событие Н — это множество, которое одновременно принадлежит и X , и Y . Иначе говоря, Н пересекается и с событием X , и с Y .

Тогда событие Н может быть представлено как сумма пересечений событий X и Н и Y и Н (см. рисунок).

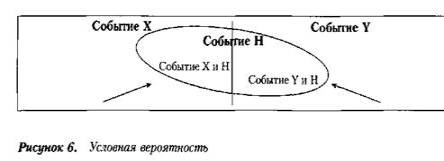
Далее, введем событие (Х/Н), которое следует читать: X при условии свершения события Н. Соответственно событие ( Y / H ): Y при условии свершения события Н.

Вероятность этих событий называют условной.

Условная вероятность — это оценка возможности наступления некоторого события при условии осуществления определенных других.

Проиллюстрировать ее определение можно на примере опыта: выбор наугад фигуранта из некоего справочника действующих трейдеров, для каждого из которых там указаны также пол и опыт работы. Примем обозначения:

•        событие X: трейдер — женщина;

•        событие Y: трейдер — мужчина;

•        событие Н: трейдер с более чем 5-летним опытом работы.

Тогда событие Х/Н — это случайно избранный фигурант оказался женщиной при условии, что попался опытный трейдер.

И событие Y / H — случайно фигурант оказался мужчиной при условии, что попался опытный трейдер.

Очевидно, что выбор наугад может пасть на одну из четырех независимых категорий трейдеров: женщина с опытом, женщина-новичок, муж чина с опытом и мужчина-новичок.

Поинтересуемся условной вероятностью события Р( Х/Н): трейдер оказался женщиной при условии, что попался опытный трейдер (т.е. событие трейдер — женщина с опытом).

По существу, задача состоит в том, чтобы вычислить долю женщин, обладающих нужным опытом работы, в общем объеме опытных трейдеров, числящихся в данном справочнике. В этом смысле все множество опытных трейдеров Н становится своего рода Новым Пространством Элементарных Событий (НПЭС).

Решение выражается формулой, которую принято рассматривать как исходное определение условной вероятности:

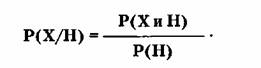
Здесь

Р( Х/Н) — условная вероятность интересующего события;

Р( Х и Н) — вероятность того, что женщина - трейдер окажется

опытной;

Р( Н) — вероятность того, что при выборе попадется опытный

трейдер (женщина или мужчина).

Как видно из рисунка:

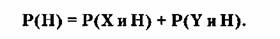
Тогда вычисление вероятности можно проводить по другой формуле, которая известна как теорема Байеса. Она справедлива и для общего случая ряда независимых событий X , Y ... Z:

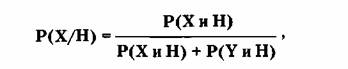
где Р( Х/Н) — вероятность события X при условии наступления события Н;

Р( Х и Н) — вероятность одновременного осуществления событий X и Н;

P ( Y и Н) — вероятность одновременного осуществления событий Y и Н.

Если, например, события X и Н независимы (не пересекаются), то:

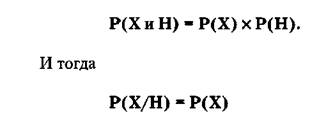
и

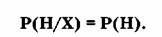
Подчеркнем, что условная вероятность событий (Х/Н) или ( Y / H ) рассматривается не на всем первоначально обозначенном пространстве элементарных событий ( X и Y ), а лишь на той его части, которая ограничена множеством события Н. Поэтому термин при условии (Х/Н) не всегда означает одновременно ( X и Н).

Дело в том, что именно множество Н, как уже отмечалось, становится новым пространством элементарных событий (НПЭС), которое входит со ставной частью в первоначальное ПЭС ( X и Y ).

В силу указанной причины событие Н называют также приведенным пространством, являющимся подпространством ПЭС.

Вот почему в общем случае условная вероятность Р( Х/Н) отличается от Р(Х) и Р(ХиН).