Удачливость. Suum cuique — каждому свое

 Это и об удачливости тоже.

Под этим явлением принято понимать кажущееся присутствие в жизни человека неких неведомых сил, которые складывают для него обстоятельства, события и возможности во благо или во зло**.

В дополнительном измерении действие этих сил проявляется как некая тенденция к возникновению повышенного числа успешных исходов в сравнении с математическим ожиданием в заданных условиях и на ограниченных участках испытаний.

Степень удачливости игрока проявляется в его индивидуальной предрасположенности к тому, что при прочих равных условиях исходы испытаний имеют тенденцию складываться более или менее «успешно».

Для дальнейших пояснений рассмотрим в качестве примера одну из моделей, которые в теории вероятностей называют урновыми. С их помощью можно получить представление об одном важном эффекте, который связывают с удачливостью. Это так называемый эффект выбора. Проведем следующие опыты.

Опыт А : классический вариант с двумя урнами *.

Имеются две урны с красными (а) и черными (в) шарами. Общее соотношение объемов этих урн n / m . В первой урне содержится al и в 1 шаров, во второй — а2 и в2. Производится последовательная выемка шаров случайным образом с возвращением: вначале случайно определяется урна, а затем из нее вслепую вынимается шар, который после выяснения цвета возвращается обратно. Красные и черные шары везде одинаковы, но каждая из урн характеризуется собственным соотношением тех и других шаров.

Интересуемся условной вероятностью события: если первый выбор пал на черный, то второй шар тоже окажется черным.

Эта схема рассматривается нами как модель следующей ситуации: имеется две группы (две урны) начинающих трейдеров, которые представлены в соотношении n : m ( n < m ).

Работе представителей первой урны (п везунков) сопутствует успех, который характеризуется тем, что на прибыльные операции ( al ) у них приходится меньше убыточных (в1), т. е. al > в1.

Вторая группа — m неудачников: у них убыточных операций (в 2 ) больше, чем прибыльных а2, т.е. а2 < в2.

Каждый из трейдеров в дилинговом зале может быть отнесен к одной из двух подгрупп, которые находятся в соотношении, — пит. Но мы не знаем, кто есть кто, и ожидаем первого практического результата.

Конечно, случайностью будет то, у кого из трейдеров первая же операция завершится неудачей: это может случиться с представителем любой подгруппы. Однако, зарегистрировав данное событие, мы затем обращаем на этого трейдера особое внимание, задавшись правомерным вопросом: какова вероятность того, что следующий убыточный результат вновь будет принадлежать тому же фигуранту?

Это условная вероятность Р( рр/р), потому что она относится к событию, обусловленному совершенно определенными обстоятельствами: если первый выбор пал на черный, то второй шар тоже окажется черным.

По известной формуле условной вероятности:

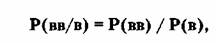
где Р( вв) — вероятность того, что черные шары окажутся при первой и второй выемках;

Р( в) — вероятность того, что при первой выемке окажется черный шар.

Можно найти, что:

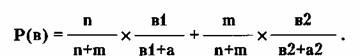
Тогда

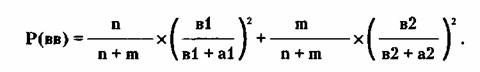
Для конкретного расчета допустим, что действует известная из практики обучения пропорция п : m = 1: 9 (т.е. из 100 начинающих трейдеров 10 везунков и 90 неудачников). Допустим, что удачливость везунков выражается соотношением: на 3 успешных операции приходится 2 убыточных (60% успеха), а у неудачников это соотношение обратное —1:4 (20% успеха)*.

Получим

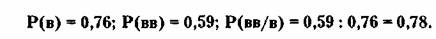
Таким образом, Р( вв/в) > Р(в). Это значит, что в сравнении с вероятностью неудачи в самый первый раз, когда трейдер начинал, так сказать, с чистого листа, здесь можно видеть возрастание вероятности неудачи при условии провала предыдущей операции.

Не правда ли, возникает отчетливое ощущение, что налицо эффект последействия. Если это так, то мы приходим к противоречию данного расчета с исходным допущением о независимости исходов от истории.

Но можно на этот счет не беспокоиться: это ощущение — неверное.