Теоремы о возвращении в начало координат: волна

 Оценки возможной продолжительности тренда дают существующие теоремы о возвращении в начало координат. Они рассматривают смену времени удачливости периодом невезучести (и наоборот), что на графике движения выражается возвращением точки блуждания на нулевую отметку.

О периодичности повторных возвращений можно судить по частоте ничьих (н). Поскольку, как мы знаем, г должно быть четным числом, то удобнее было бы обозначать общее число испытаний как 2г (г = 2г, где г — это целое положительное число, не равное нулю: 1, 2, 3 и т.д.).

Здравый смысл подсказывает, что чем больше испытаний, тем больше должно быть возвращений в начало координат, т.е. ничьих (н).

Это верно. Но зависимость здесь не является прямо пропорциональной. И на этот счет у В. Феллера приводится доказательства двух важных теорем*.

Теорема 1. Основной является формула вероятности Р( н/2г) того, что точка вернется в начало координат н раз в течение периода испытаний 2г:

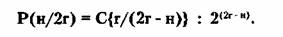
Можно рассчитать, что для всех испытаний, продолжительностью 2г, справедливо неравенство:

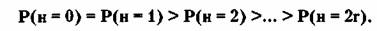
Если его проанализировать, можно сделать следующие выводы.

1. Р( н = 0) = Р(н = 1) означает, что наиболее вероятным исходом будет полное отсутствие (н = 0) либо только одно (н = 1) возвращение в начало координат.

2.     Р( н = 1) > Р(н = 2) >... > Р( н = 2г) означает, что одно возвращение более вероятно, чем два (н = 2). Но, в свою очередь, это событие более вероятно, чем три возвращения и т.д.

Повышенная вероятность меньшего числа возвращений объясняется тем, что если уж точка отклонилась от нулевого уровня, то ей труднее вернуться обратно в начало координат, а тем более на противоположную сторону графика.

Таким образом, наиболее вероятными конфигурациями случайного блуждания являются тренд и полуволна (см. рисунок).

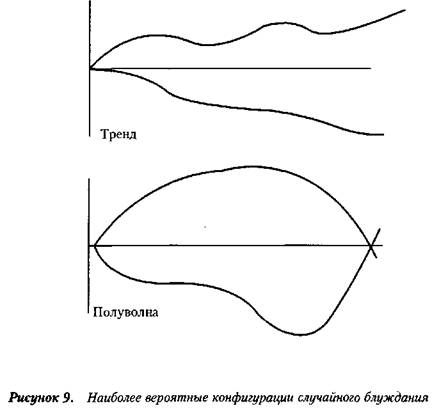
Согласно первой теореме о возвращении, наиболее вероятными конфигурациями при случайном блуждании являются тренд и полуволна.

Как видим, эти результаты полностью согласуются с первой теоремой арксинуса.

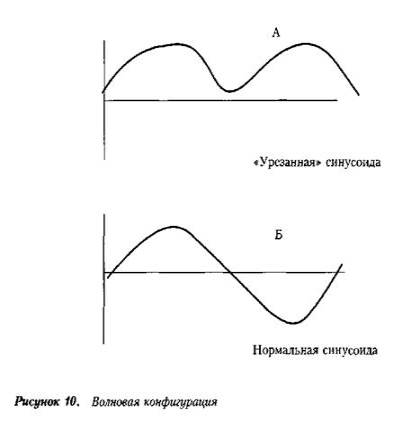
Очевидно, что точку завершения полуволновой конфигурации можно рассматривать как начало координат для последующего развития событий. Тогда следующая полуволна (см. рисунок) приведет к волне вида урезанной синусоиды (А) или ее нормального варианта (Б).

Теорема 2. Это конкретная оценка вероятностей, которые составляют содержание теоремы 1.

Речь идет о вероятности события, определенного как не более чем не которое заданное число возвращений в начало координат.

Как раз об этом и говорит теорема 2.

В более строгой формулировке она звучит так: для некоторого фиксированного числа j > 0 вероятность того, что в серии испытаний от 0 до 2г точка блуждания вернется в начало координат не более j x (2г)0,5 раз (при возрастании 2г до бесконечности), стремится к следующей величине:

i

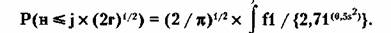
s =0

Мы не будем анализировать эту функцию, а лишь подчеркнем, что вероятность пересечения нулевой отметки будет возрастать пропорционально не 2г, а квадратному корню из этой величины (2г1/2).

Эта формула означает, что и длина волны будет также возрастать по мере увеличения числа испытаний.