Теорема Байеса и вероятность совпадения

 Обратим внимание на то, сколь значительным может быть даже чисто случайное отклонение. Даже, если в ходе проверки успешно сработают все 25 сигналов, это тоже может быть случайностью, хотя и маловероятной. Необходимую ясность здесь способны внести только дополнительные эксперименты.

Но до того, как они начнутся, оценка вероятности успеха вызывает к себе лишь некоторую степень доверия, которая в свою очередь основана на интуиции, здравом смысле или каких-то иных гипотетических соображениях наблюдателя.

Чтобы отличать такое сугубо личное отношение от статистически обоснованных оценок, иногда говорят о персональных вероятностных суждениях. Тем самым подчеркивается факт выражения личной (персональной) степени доверия наблюдателя к исходной (априорной) оценке вероятности.

Конечно, последующие дополнительные эксперименты могут укреплять или ослаблять эти персональные оценки.

Уже представленную ранее теорему Байеса об условной вероятности и принято использовать для внесения изменений, соответствующих результатам экспериментов.

Теорема Байеса является одним из оснований, которое используется для внесения изменений в исходные гипотетические представления в результате дополнительной экспериментальной проверки.

Рассмотрим развитие ситуации в нашем прежнем примере: после некоторой доработки разработчик уточнил свое утверждение. Теперь он уверен, что его система способна давать результат на уровне 7 успехов из каждых 10 генерированных сигналов.

Таким образом, скептик должен предварительно как-то определить свое личное отношение к двум гипотезам: нулевой и 0,7. В такой ситуации удобно использовать оценки в виде шансов в пользу той или иной гипотезы (как это обычно делается в букмекерских конторах).

Скептик посоветовался с собой и решил, что нулевой гипотезе (р = 0,5) он доверяет на 98%, а гипотезе р = 0,7 — лишь на 2%. Это и есть персональные вероятности: Р( перс; р = 0,5) = 0,98 и Р(перс; р = 0,7) - 0,02.

Здесь важно подчеркнуть, что гипотезы, которые относятся к вариантам р = 0,5 и р = 0,7, должны составлять пространство элементарных событий. Это значит, что если степень доверия к одному из них выражается как Р( перс), то степень доверия к другому событию обязана стать i - Р(перс).

В данном случае имеем крайне скептическое соотношение — 49:1 в пользу нулевой гипотезы.

Далее, скептик проконтролировал 25 экспериментов по генерированию сигнала и зафиксировал 17 успехов, что соответствует р( ехр) = 0,68.

Подвели итог.

Разработчик посчитал, что он почти доказал свое утверждение. Но скептик сомневается: ведь результат-то оказался на границе лишь 75%-ного доверительного интервала.

Тем не менее, скептик не может игнорировать полученные в ходе эксперимента данные и готов внести в исходные шансы (49:1) коррективы, но только на основе научной аргументации.

В этом качестве и служит теорема Байеса: необходимо рассчитать степень доверия к двум гипотезам (р = 0,5 и р = 0,7) при условии, что про изошло событие р(ехр) = 0,68.

Тогда скорректированные шансы в пользу нулевой гипотезы:

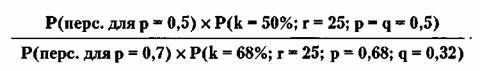
Можно посчитать самостоятельно или найти по таблицам*, что:

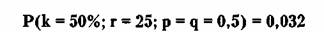
и

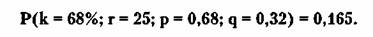
Тогда экспериментальное соотношение шансов двух гипотез становится равным примерно:

(49 х 0,032) / (1 х 0,165) = 9,50,

т.е. 95/10, или примерно 9/1, вместо прежних 49/1.

Но допустим, что разработчик проявил настойчивость, и к тому же ему сопутствует удача: еще в одной дополнительной серии из 25 экспериментов он вновь получил 17 успехов.

Скептику приходится вносить поправку теперь уже в предыдущую оценку:

(95 х 0,032) / (10 х 0,165) = 1,84,

т.е. уже получается величина примерно 9/5 вместо прежних 9/1.

Наконец, скептик договорился с неутомимым исследователем провести третью решающую серию из 25 экспериментов.

Разработчику снова повезло: те же 17 успехов.

После окончательной поправки скептиком своего отношения под влиянием трех экспериментальных серий по 25 испытаний и с 17 успехами в каждой серии получаем соотношение:

Это означает, что в оценке скептика произошел перелом: впервые он вынужден оценивать шансы гипотезы р = 0,7 более предпочтительно, чем ну левой. Если до этого шансы в пользу неблагоприятной для разработчика нулевой гипотезы были 9/5, то сейчас это уже примерно 2/5, т.е. произошел сдвиг от р = 0,5 в пользу р = 0,7.

Между прочим, для этого потребовались три успешные серии подряд: тут даже самый заядлый скептик-экстремист (98 против 2) должен немедленно сдаваться. Или — потребовать еще серию, а может, и не одну с тем, чтобы сдаться при оценке, скажем, 1:1000.

Однако никто не сможет предугадать исход заранее. И даже, если все опять сложится благополучно для трейдера-исследователя, это можно рассматривать просто как невероятное везение: вот такой у него, мол, замечательный арксинус!

 тех результатов, с которыми приходится сталкиваться в различных исходных условиях, позволяет делать вполне уверенные оценки, касающиеся эффективности конкретно применяемых систем работы.