Статистическая (безусловная) вероятность

Изменение условий испытания меняет и ПЭС. Если, скажем, испытание заключается в том, чтобы бросить монету дважды, то пространство элементарных событий будет включать в себя уже четыре элементарных события: орел-орел, решка-решка , орел-решка и решка-орел. Для г испытаний ПЭС будет содержать 2Г событий.

Случайная величина (переменная) — некоторая функция, определенная на пространстве элементарных событий через исходы некоторого опыта или эксперимента*.

Статистическая (безусловная) вероятность — численное значение, характеризующее меру неопределенности и возможности какого-то события или значения переменной величины.

Вероятность изменяется в пределах от 0 до 1:

•       0 — это оценка события как статистически определенного в качестве невозможного, сколько бы одинаковых испытаний не про водилось;

•       1 — оценка события как статистически определенного в качестве неизбежного, сколько бы одинаковых испытаний не проводилось;

•       0,5 означает статистическую неопределенность, когда при любом числе испытаний, скажем, имеющих только два исхода (событие есть или его нет), каждый раз следует в равной мере ожидать как свершения события, так и его отсутствия.

Условная вероятность — мера случайности события, которое рассматривается при условии одновременного совершения какого-то другого случайного события.

Шансы — это еще одна форма выражения вероятностной оценки, наиболее часто используемой при интуитивно-психологическом подходе, особенно там, где вероятности некоторого события X целесообразно взвешивать по дихотомии исходов за и против.

Шансы, что некоторое событие X произойдет, принято выражать в форме:

а/Ь,

где а — любое число, характеризующее оценку за то, что событие X произойдет;

b — любое число, характеризующее оценку против того, что событие X произойдет.

Например, говорят, что шансы на успех в игре против рынка — 50:50.

Если известны величины а и b, то вероятность того, что событие X про изойдет, вычисляется по формуле:

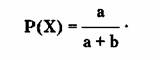
Можно видеть, например, что для события X, шансы которого оцениваются как 50:50, вероятность будет равна 0,5.

С другой стороны, если мы знаем значение вероятности Р(Х), то шансы в его пользу можно рассчитать по обратной формуле:

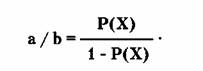
Иногда, в обыденной жизни оценки шансов и вероятности интересующего события ошибочно отождествляются. Так, если шансы на успех оцениваются как 1:10, то это вовсе не значит, что вероятность неудачи равна 0,1. Можно посчитать по формуле, приведенной выше, что на самом деле это 0,09.

Шансы — это не вероятность, а соотношение, так сказать, голосов за и против. Поэтому вместо 50:50 можно в равной мере использовать 1:1 или 49:49. Существо оценки не изменится — соотношение за и против со хранится.