Foreign Exchange Operations - Коэффициент регрессии

Оглавление >>> Производные финансовые и товарные инструменты

Если бы значение коэффициента регрессии не зависело от единиц измерения, в которых выражены коррелируемые признаки, то этот коэффициент мог бы служить мерой тесноты корреляционной связи. Коэффициент корреляции в свою очередь можно рассматривать как коэффициент регрессии, выраженный в нормированных отклонениях для обоих признаков (не в единицах измерения коррелируемых признаков), т. е. коэффициент корреляции представляет собой стандартизированный коэффициент регрессии.

Вместе с тем коэффициент регрессии можно определить и без знания вычисленного коэффициента корреляции. Для этого в формуле (5.7) вместо rух подставим начальную формулу коэффициента корреляции из их ряда (5.1):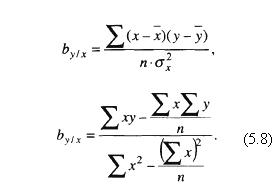

При криволинейной зависимости решение задачи выявления меры связи между признаками затрудняется. Сложность состоит в выборе (предварительном) математической формы для линии регрессии, основанном на понимании характера (природы) изучаемой совокупности (парабола, гипербола и т.п.).

Общим формальным выражением для прямолинейной и криволинейной корреляционной связи является теоретическое корреляционное отношение.

Для гипотетически принятой формы связи вычисляется показатель, выражающий численное значение тесноты связи: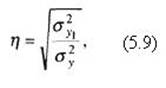

где Q2y1 – дисперсия, вычисленная для теоретических значений у (у1);

Q2y – дисперсия, вычисленная для эмпирических значений у.

Продолжение >>> Корреляционное отношение

Главная Софт Литература Читайте на сайте Контакты