Foreign Exchange Operations - Анализ временных рядов, численные методы, математика непрерывных процессов

Оглавление >>> Производные финансовые и товарные инструменты

При корреляционном анализе предполагается, что если два ряда данных возрастают и убывают одновременно, то связь между ними (их корреляция) – положительна; при противоположном одновременном изменении корреляция – отрицательна; при одновременном независимом изменении этих рядов корреляция обращается в ноль (величины не коррелируют).

Если коэффициент корреляции равен единице, то имеется прямолинейная функциональная зависимость. Чем теснее связь, тем значение коэффициента корреляции ближе к единице. Практически коэффициент корреляции крайних своих значений (1; –1) никогда не принимает, лишь приближается к единице при высокой степени тесноты связей.

Корреляционная связь проявляется в совокупности случайных величин и только в среднем. "Так называемая "корреляционная модель" предполагает, что распределение обоих коррелируемых признаков носит случайный характер, тяготеет к нормальной кривой, или к нормальной корреляции.

Корреляционный анализ позволяет измерить тесноту связи статистических признаков, определить (переход к регрессионному анализу) форму этой связи и провести углубленно исследование последней. Вопрос о вероятностной оценке полученной характеристики тесноты связи в корреляционном анализе решается с помощью приемов выборочного метода.

Достаточно полным выражением тесноты связи по двум признакам в корреляционном анализе выступает ряд формул: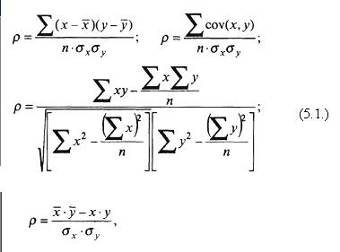

где р – коэффициент корреляции;

x – значения признака-фактора (независимой величины);

у – значения коррелируемого признака (зависимой переменной) с фактором-признаком;

n – число пар сопоставимых значений признаков;

Qx – величина среднеквадратического отклонения ряда х; Qy – величина среднеквадратического отклонения ряда у.

Рассмотрим отдельные конкретные, частные способы расчета коэффициентов связи в рамках корреляционного анализа.

Продолжение >>> Коэффициент корреляции рангов Спирмэна

Главная Софт Литература Читайте на сайте Контакты